本文实例讲述了Python通过TensorFLow进行线性模型训练原理与实现方法。分享给大家供大家参考,具体如下:
1、相关概念
例如要从一个线性分布的途中抽象出其y=kx+b的分布规律
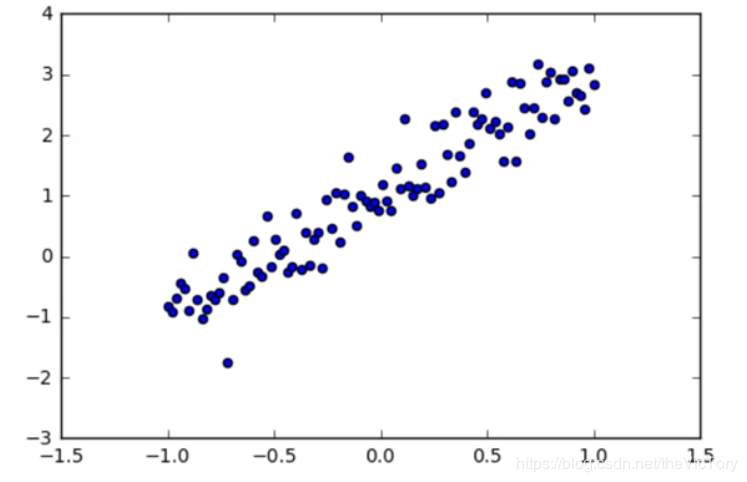
特征是输入变量,即简单线性回归中的 x 变量。简单的机器学习项目可能会使用单个特征,而比较复杂的机器学习项目可能会使用数百万个特征。
标签是我们要预测的事物,即简单线性回归中的 y 变量。
样本是指具体的数据实例。有标签样本是指具有{特征,标签}的数据,用于训练模型,总结规律。无标签样本只具有特征的数据x,通过模型预测其y值。
模型是由特征向标签映射的工具,通过机器学习建立。
训练是指模型通过有标签样本来学习,确定其参数的理想值。通俗理解就是在给出一些样本点(x,y),总结其规律确定模型y=kx+b中的两个参数k、b,进而利用这个方程,在只给出x的情况下计算出对应的y值。
损失是一个数值,用于表示对于单个样本而言模型预测的准确程度。预测值与准确值相差越大,损失越大。检查样本并最大限度地减少模型损失的过程叫做经验风险最小化。L1损失是标签预测值与实际值差的绝对值。平方损失是样本预测值与实际值的方差。
模型的训练是一个迭代的过程,首先对模型的参数进行初始参数,得到一个初步模型并计算出特征对应的标签值,然后经过比对计算出损失。之后对模型的参数进行调整,之后再进行预测、计算损失,如此循环直到总损失不再变化或变化很缓慢为止,这时称该模型已经收敛。
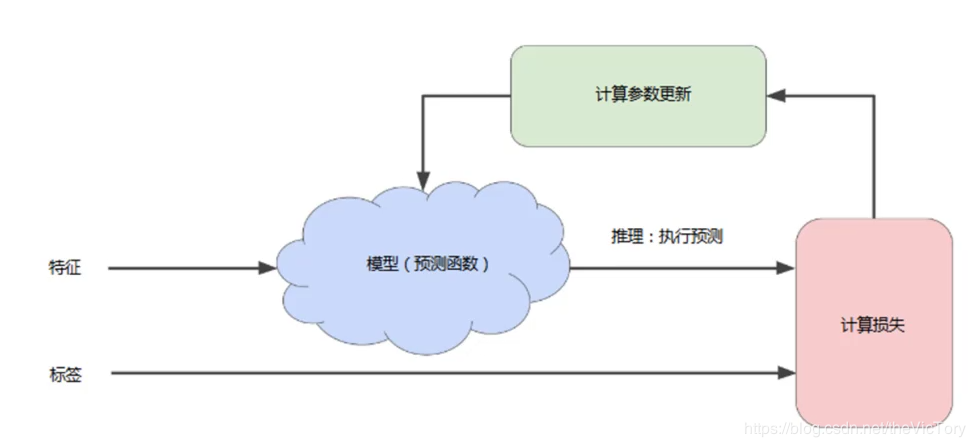
类似于对于一个二次函数,通过不断调整x的值,找到其函数的极值点,在该点处函数的变化率为0。那么如何找到极值点,可以采用梯度下降法,即对于函数曲线,朝着其梯度值减少的方向(负梯度)探索便可以最快找到极值点。
前向传播:根据输入计算输出值。反向传播:根据优化器算法计算内部变量的调整幅度,从输出层级开始,并往回计算每个层级,直到抵达输入层。
在梯度下降法中,批量是指单次迭代中用于计算梯度的样本数。随机梯度下降法是指每次随机选择一个样本进行梯度计算。
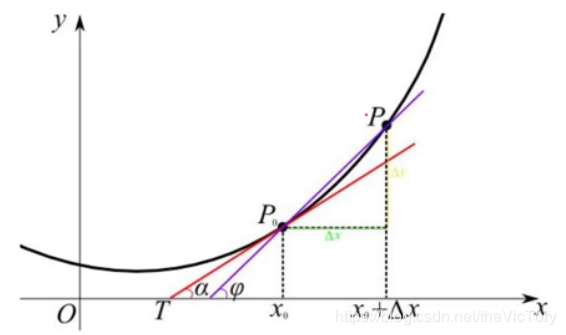
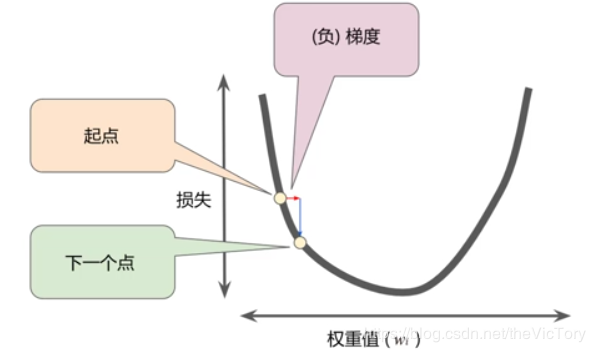
那么朝探索的方向前进多少比较合适?这就涉及到学习速率,用梯度乘以学习速率就得到了下一个点的位置,也叫做步长,如果步长过小,那么可能需要许多次才可到达目标点,如果步长过大,则可能越过目标点。
这种参数需要人为在学习之前设置参数,而不是通过训练得到的参数,这种参数叫做超参数。超参数是编程人员用于对机器学习进行调整的旋钮。
2、算法设计与训练
通过Tensor FLow进行训练的步骤主要有:准备数据、构建模型、训练模型、进行预测
准备数据
使用的数据可以是从生活中的数据经过加工而来,也可以是人工生成的数据集,例如产生y=2x+1附近的随机数点:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
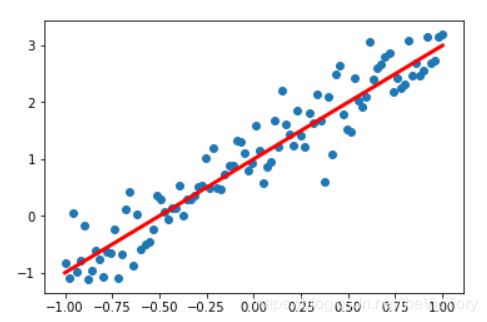
#在jupyter中设置图像的显示方式inline,否则图像不显示%matplotlib inline import tensorflow as tfimport numpy as np #Python的一种开源的数值计算扩展import matplotlib.pyplot as plt #Python的一种绘图库 np.random.seed(5) #设置产生伪随机数的类型x=np.linspace(-1,1,100) #在-1到1之间产生100个等差数列作为图像的横坐标#根据y=2*x+1+噪声产生纵坐标#randn(100)表示从100个样本的标准正态分布中返回一个样本值,0.4为数据抖动幅度y=2*x+1.0+np.random.randn(100)*0.4 plt.scatter(x,y) #生成散点图plt.plot(x,2*x+1,color='red',linewidth=3) #生成直线y=2x+1 |
在jupyter中绘制出了人工数据的散点图与曲线如下:
构建模型
|
1
2
3
4
5
6
7
8
9
10
11
12
|
#定义函数模型,y=kx+bdef model(x,k,b): return tf.multiply(k,x)+b#定义模型中的参数变量,并为其赋初值k=tf.Variable(1.0,name='k')b=tf.Variable(0,name='b') #定义训练数据的占位符,x为特征值,y为标签x=tf.placeholder(name='x')y=tf.placeholder(name='y')#通过模型得出特征值x对应的预测值ypyp=model(x,k,b) |
k、b的初始值并不会影响最终结果的得到,所以可以随意指定一个值。
训练模型
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
#训练模型,设置训练参数(迭代次数、学习率)train_epoch=10rate=0.05#定义均方差为损失函数loss=tf.reduce_mean(tf.square(y-yp))#定义梯度下降优化器,并传入参数学习率和损失函数optimizer=tf.train.GradientDescentOptimizer(rate).minimize(loss) ss=tf.Session()init=tf.global_variables_initializer()ss.run(init) #进行多轮迭代训练,每轮将样本值逐个输入模型,进行梯度下降优化操作得出参数,绘制模型曲线for _ in range(train_epoch): for x1,y1 in zip(sx,sy): ss.run([optimizer,loss],feed_dict={x:x1,y:y1}) tmp_k=k.eval(session=ss) tmp_b=b.eval(session=ss) plt.plot(sx,tmp_k*sx+tmp_b) ss.close() |
迭代次数是人为规定模型要训练的次数。学习率不能太大或太小,根据经验一般设置在0.01到0.1之间
采用均方差为损失函数,square求出y-yp的平方,再通过reduce_mean()求出平均值
再将之前人工生成的数据输入到占位符时,通过zip()函数先将每个sx,sy对应压缩为一个二维数组,然后对100个二维数组进行遍历取出并分别填充到占位符x、y,使会话运行优化器optimizer进行迭代训练。
可以看到运行结果如下,预测的曲线慢慢向分布的散点进行拟合
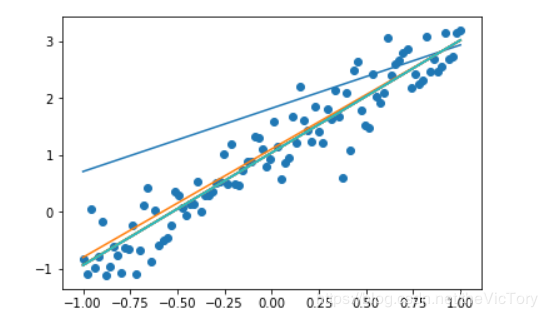
进行预测
根据函数模型,y=kx+b,将得到的参数k、b和特质值x带入即可得到标签y的预测值
3、数组操作
Numpy是一个支持大量的维度数组与矩阵运算的python库,通过它可以很便捷地将数据转换为数组并进行操作。np类型的shape属性可以输出数组的维数构成。可以通过np.T对数组进行转置,或者np.rashape(3,2)将数组转换为目标形状。例子如下
|
1
2
3
4
5
6
7
8
9
10
11
|
scalar=1scalar_np=np.array(scalar) #将标量转化为np的数组类型print(scalar_np.shape) #只有np才有shape属性,标量对应的shape输出为() #二维以上的有序数组才可以看作矩阵matrix=[[1,2,3],[4,5,6]]matrix_np=np.array(matrix) #将list转化为np矩阵print('二维数组:',matrix) #输出为单行数组print('矩阵形式:\n',matrix_np) #结果将以多行矩阵的形式输出print('矩阵转置:\n',matrix_np.T)print('shape值',matrix_np.shape) |


矩阵可以直接进行+、-、*运算,但前提是两个矩阵的形状相同。矩阵还可以进行叉乘运算,要求前者的行与后者的列相同,例子如下,运行结果为右上图:
|
1
2
3
4
5
|
ma=np.array([[1,2,3],[4,5,6]])mb=np.array([[1,2],[3,4],[5,6]])print(ma+ma)print(ma*ma) #矩阵点乘print(np.matmul(ma,mb)) #矩阵叉乘 |
4、多元线性回归模型
多元线性回归模型就是在一元线性函数y=kx+b的基础上,对于不同的特质值x1,x2...xn,将参数k扩展为多个,即y=k1x1+k2x2+...knxn+b,进而求解n+1个参数的过程。其中n个k与x相乘可以看作是两个矩阵相乘。例如下面是一个房价预测的简单模型,有x1~x12共12个影响房价的特质值,对应的标签为房价,通过多元线性模型求解对应的参数k1~k12、b,从而对房价进行预测:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
|
%matplotlib notebook import tensorflow as tfimport matplotlib.pyplot as pltimport numpy as npimport pandas as pdfrom sklearn.utils import shuffle #利用pandas读取数据csv文件data=pd.read_csv('D:/Temp/data/boston.csv',header=0)#显示数据摘要描述信息#print(data.describe())data=np.array(data.values) #将data的值转换为np数组for i in range(12): #将所有数据进行归一化处理 data[:,i]=data[:,i]/(data[:,i].max()-data[:,i].min())x_data=data[:,:12] #截取所有行,0到11列作为特质值xy_data=data[:,12] #截取所有行,第12列作为标签值y x=tf.placeholder(tf.float32,[None,12],name='x') #None代表行数不确定,12代表一行特征值有12个子数据y=tf.placeholder(tf.float32,[None,1],name='y') with tf.name_scope('Model'): #定义命名空间 k=tf.Variable(tf.random_normal([12,1],stddev=0.01),name='k') b=tf.Variable(1.0,name='b') def model(x,k,b): return tf.matmul(k,x)+b #数组k,x进行叉乘运算再加上b yp=model(x,k,b) #定义超参数:训练次数、学习率、损失函数train_epochs=50learning_rate=0.01with tf.name_scope('Loss'): loss_function=tf.reduce_mean(tf.square(y-yp))#使用梯度下降法定义优化器 optimizer=tf.train.GradientDescentOptimizer(learning_rate).minimize(loss_function) ss=tf.Session()init=tf.global_variables_initializer()ss.run(init)loss_list=[] for _ in range(train_epochs): loss_sum=0 for(xs,ys)in zip(x_data,y_data): xs=xs.reshape(1,12) #调整数据的维数格式以匹配占位符x ys=ys.reshape(1,1) _,loss=ss.run([optimizer,loss_function],feed_dict={x:xs,y:ys}) loss_sum+=loss shuffle(x_data,y_data) #每轮循环后,打乱数据顺序 k_tmp=k.eval(session=ss) b_tmp=b.eval(session=ss) print('k:',k_tmp,',b:',b_tmp) loss_avg=loss_sum/len(y_data) #求每轮的损失值 loss_list.append(loss_avg) plt.plot(loss_list) |
注:
pandas是一个python库,可以提供高性能且易使用的数据结构与数据分析工具,可以从csv、excel、txt、sql等文件中读取数据,并且将数据结构自动转换为Numpy多维数组。
在使用梯度下降法进行多元线性回归模型训练时,如果不同的特征值取值范围相差过大(比如有的特质值取值为0.3~0.7,有点特质值在300~700),就会影响训练结果的得出。因此需要对数据进行归一化处理,即用特征值/(最大值-最小值),也就是通过放缩将数据都统一到0~1之间。
通过tf.name_scope()定义命名空间,定义的变量名只在当前空间内有效,防止命名冲突。
在初始化变量k时,通过tf.random_normal()从正太分布[1,12]之间随机选取一个值,其方差stddev=0.01
由于在定义占位符时x为[None,12]类型的二维数组,所以在填充数据时需要通过xs.reshape(1,12)将数据xs重新排列为一维含有12个元素,二维含有1个子数组的二维数组,同理,y也需要转换。
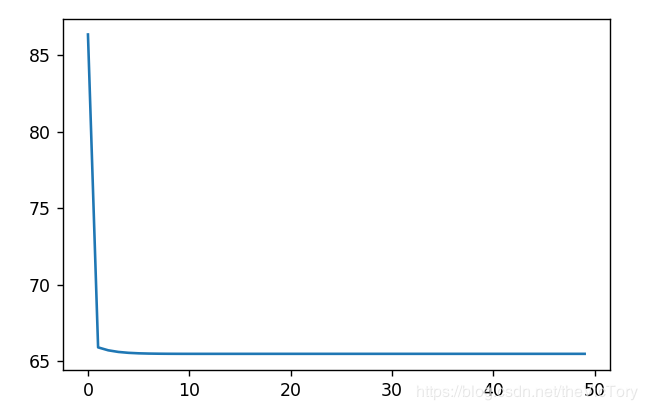
实现定义loss_list用于保存损失值,在每轮训练后求出损失值的平均值保存到loss_list,最后将其打印成一幅图,可以看到损失值从一开始急速下降,直到最后变化趋于平缓。
运行结果如下,截取部分的参数值以及损失值的曲线:

希望本文所述对大家Python程序设计有所帮助。
原文链接:https://blog.csdn.net/theVicTory/article/details/95238260





